Ultrarelativistic limit

In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light $c$ .

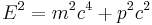Max Planck showed that the relativistic expression for the energy of a particle whose rest mass is $m$ and momentum is $p$ is given by $E^2 = m^2 c^4 %2B p^2 c^2$ . The energy of an ultrarelativistic particle is almost completely due to its momentum ( 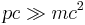$p c \gg m c^2$ ), and thus can be approximated by 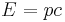$E = p c$ . This can result from holding the mass fixed and increasing p to very large values (the usual case); or by holding the energy E fixed and shrinking the mass m to negligible values. The latter is used to derive orbits of massless particles such as the photon from those of massive particles (cf. Kepler problem in general relativity).

In general, the ultrarelativistic limit of an expression is the resulting simplified expression when 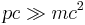$p c \gg m c^2$ is assumed. Or, similarly, in the limit where the Lorentz factor is very large ( 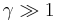$\gamma \gg 1$ ).^[1]

1 Accuracy of the approximation
2 Other limits
3 See also
4 References

Accuracy of the approximation

For calculations of the energy of a particle, the relative error of the ultrarelativistic limit for a speed 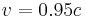$v = 0.95 c$ is about 10%, and for 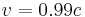$v = 0.99 c$ it is just 2%. For particles such as neutrinos, whose γ (Lorentz factor) are usually above 10⁶ ( $v$ very close to c), the approximation is essentially exact.

Other limits

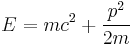The opposite case is a so-called classical particle, where its speed is much smaller than $c$ and so its energy can be approximated by $E = m c^2 %2B \frac{p^2}{2m}$ .

References

^ Dieckmann, ME (April 2005). "Particle simulation of an ultrarelativistic two-stream instability". Physical Review Letters 94 (15): 155001. Bibcode 2005PhRvL..94o5001D. doi:10.1103/PhysRevLett.94.155001. PMID 15904153.

Ultrarelativistic limit

Contents

Accuracy of the approximation

Other limits

See also

References